The example of EM algorithm to solve the problem in page 137 of Machine Learning book(Chinese Edition) written by Tom M. Mitchell.
##EM算法一般表述:
当有部分数据缺失或者无法观察到时,EM算法提供了一个高效的迭代程序用来计算这些数据的最大似然估计。在每一步迭代分为两个步骤: 期望(Expectation)步骤和最大化(Maximization)步骤,因此称为EM算法。
假设全部数据Z是由可观测到的样本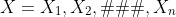和不可观测到的样本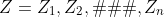组成的,则Y = X∪Z。
EM算法通过搜寻使全部数据的似然函数Log(L(Z;h))的期望值最大来寻找极大似然估计,注意此处的h不是一个变量,而是多个变量组成的参数集合。此期望值是在Z所遵循的概率分布上计算,此分布由未知参数h确定。然而Z所遵循的分布是未知的。EM算法使用其当前的假设h‘代替实际参数h,以估计Z的分布。
 = E [ ln P(Y|h') | h, X ])
EM算法重复以下两个步骤直至收敛。
步骤1:估计(E)步骤:使用当前假设h和观察到的数据X来估计Y上的概率分布以计算$Q( h' | h )$。
 \leftarrow {E[ ln P(Y|h') | h, X ]})
步骤2:最大化(M)步骤:将假设h替换为使Q函数最大化的假设h':
})
##问题 有N个样本x,每个样本产生规则是:
每个样本x是服从某个正态分布k(既样本x是用某个正态分布k产生)
现在已知样本个数N,样本值X,正态分布个数K,K个正态分布的方差都相同,求每个正态分布的均值?
对应到现实问题就是:
抽取N个同学的身高,男女同学的身高服从正态分布,假设两个正态分布的方差相同,分别求出这两个正态分布的均值?
##参考 EM算法实现